关于减肥药的那点破事－[箱线图]两组数据差异比较
作者： Excellence // 2012 年 5 月 29 日 // Excel图表 // 没有评论
朋友 @ETwise 发了篇博文： 数据分析那点统计学(1)：T检验 尽引无数数据控疯狂转发。虽然统计方法：T[学生]检验在小样本(N＜30)的两均值差异程度时堪称瑞士军刀，但基于T分布理论来推断差异发生概率，从而判定两平均数差异是否显著的该方法却有两个前提条件：
- 个体间相互独立，数据取自正态分布总体；
- 满足方差齐性。
神马『正态分布』与『方差齐性』？这概念对于非统计科班出身的数据童鞋来讲，这确实够绕的 
！亲：你的数据满足这要求不？这确实是个问题，你说对不？原博文有段内容：
在数据分析的工作中，经常用到的数据统计基本都是：均值、个数、百分比、求和等基本指标，接着从多个维度进行分析，最后刷刷地把统计的数据做成几十页PPT的分析报告，完毕后，会很自豪地说：数据分析其实很简单，那些基本统计的方法都熟练地掌握了。
基础的描述性统计指标：均值、峰度、偏倚难不成就非得要几十页PPT？难倒数据控的报告都得屁屁痛过才可以？难倒比较一下服用减肥药是否有用，这点破事也一定非艰深统计学不能胜任？其实可以肯定的告诉大家：非也！先上数据[数据来自 @ETwise 博文]
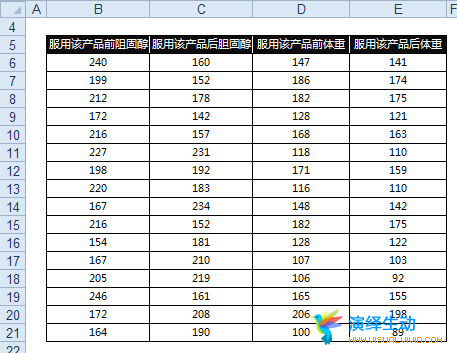
上完数据，现在上图[见下方]，对于服药前后：胆固醇和体重两个指标变化马上图示化表达出来了，虽然没有峰度、偏倚的计算，却也看得清清楚楚。同时还可粗略地看出数据是否具有对称性，分布的分散程度等信息，简单直接。
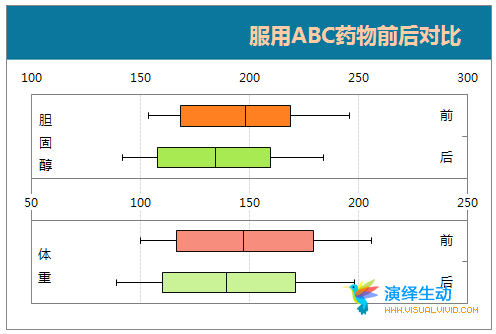
这图貌似平常所见甚少，叫作：箱线图(Box Plot & Boxplot) 也称箱须图(Box-whisker Plot)，该图于1977年由美国著名统计学家 约翰·图克(John Tukey) 发明。通过数据的五个统计量：最小值、第一四分位数[25%]、均值[中位数]、第三四分位数[75%]与最大值来描述数据的一种方法，特别适合用于多个样本间的比较。
关于本案例中图表的制作请参考《演绎生动：Excel图表》一书P312～317页内容，以及本文所附附件来学习制作。
